数据处理

原始数据集说明

用户与课程关联数据集, 行数说明

字段	名称	示例值	描述	取值范围
views	浏览记录	60%	用户对课程浏览进度	（0%，100%）
favorites	收藏记录	0	用户是否收藏课程，1 为收藏	enum(0,1)
likes	点赞记录	1	用户是否点赞课程，1 为点赞	enum(0,1)
comments	评论记录	["Loved it", "Would buy again"]	用户对课程的评论，为字符串数组	["Great product!", "Loved it", "Would buy again"]
shares	分享记录	1	用户是否分享课程，1 为分享	enum(0,1)
feedbacks	反馈记录	[ "Shipping was fast"]	用户对课程的反馈，为字符串数组	["The product was good", "Shipping was fast"]
ratings	评分记录	3	用户对课程的评分	（1，5）

中间状态，文本情感计算

处理文本情感之后的数据，示例如下：

用户编码	课程编码	浏览记录	收藏记录	点赞记录	评论记录	分享记录	反馈记录	评分记录
1	1	0.28	1	0	0.25	1	0.87	1
1	2	0.49	0	1	0.76	0	0.65	3

其中，评论记录和反馈记录通过 NLP 的情感分析，得到（0,1）之间的两位小数。偏向 1 表示正向情感。

pip install snownlp

from snownlp import SnowNLP

text1 = "这个产品真的很好用！"
s = SnowNLP(text1)
print(s.sentiments)  # 输出情感得分 0.8380894562907347


from snownlp import SnowNLP

text = "好烦啊，和参数对不上！"
s = SnowNLP(text)
print(s.sentiments)  # 输出情感得分 0.2734196629160368

计算 User-Item 的评分

在原始 ml-100k 数据集中，用户和电影之间的评分是手动打的，本项目中的实现逻辑也比较简单。计算物品或者用户的邻居逻辑都在类 CoreMath中。所以这边需要根据浏览记录、收藏记录、点赞记录、评论记录、反馈记录、评分记录等信息计算出一个评分。

实现逻辑是将所有的信息都标准化为一个 0 到 1 之间数，然后按照不同信息的重要程度给一个权重。计算出一个 1 到 5 之间的分数。这样就不需要改动原有算法的代码了。

权重分配说明：

浏览记录 (views): 虽然浏览行为重要，但它属于较为被动的行为。建议赋予较低的权重。
收藏记录 (favorites): 收藏表明用户对产品有一定的兴趣，建议赋予中等权重。
点赞记录 (likes): 点赞表示用户的积极反馈，建议赋予中等偏高的权重。
评论记录 (comments): 评论能直接反映用户的想法，建议赋予较高的权重。
分享记录 (shares): 分享表明用户愿意向他人推荐产品，建议赋予中等偏高的权重。
反馈记录 (feedbacks): 反馈通常比评论更详细，建议赋予较高的权重。
评分记录 (ratings): 评分是最直接的用户评分，建议赋予最高的权重。

权重分配建议

weights = {
    'views': 0.05,        # 浏览记录：较低权重
    'favorites': 0.1,     # 收藏记录：中等权重
    'likes': 0.15,        # 点赞记录：中等偏高权重
    'comments': 0.2,      # 评论记录：较高权重
    'shares': 0.15,       # 分享记录：中等偏高权重
    'feedbacks': 0.2,     # 反馈记录：较高权重
    'ratings': 0.15       # 评分记录：最高权重
}

代码示例

from typing import Dict
from snownlp import SnowNLP

def calculate_composite_score(
        views: float,
        favorites: int,
        likes: int,
        comments: list[str],
        shares: int,
        feedbacks: list[str],
        rating: int,
        weights: Dict[str, float] = None
) -> float:
    if weights is None:
        print("No weights provided, using default values.")
        weights = {
            'views': 0.01,
            'favorites': 0.1,
            'likes': 0.125,
            'comments': 0.175,
            'shares': 0.125,
            'feedbacks': 0.175,
            'rating': 0.29
        }
    print(f"Weights: {weights}")

    # 量化 comments 和 feedback 数据，如果列表为空则默认为0
    avg_comment_score = np.mean([SnowNLP(comment).sentiments for comment in comments]) if comments else 0
    avg_feedback_score = np.mean([SnowNLP(feedback).sentiments for feedback in feedbacks]) if feedbacks else 0

    # 格式化为两位小数
    avg_comment_score_formatted = round(avg_comment_score, 2)
    avg_feedback_score_formatted = round(avg_feedback_score, 2)

    print(f"Average comment score: {avg_comment_score_formatted}")
    print(f"Average feedback length: {avg_feedback_score_formatted}")

    # 将评分数据缩放到 0-1
    scale_rating = rating * 0.2

    # Calculate the weighted score
    score = (
            views * weights['views'] +
            favorites * weights['favorites'] +
            likes * weights['likes'] +
            avg_comment_score_formatted * weights['comments'] +
            shares * weights['shares'] +
            avg_feedback_score_formatted * weights['feedbacks'] +
            scale_rating * weights['rating']
    )

    print(f"Score: {score}")

    # Ensure the score is in the range [1, 5]
    score = max(1, min(5, score * 5))

    return round(score, 2)


# 示例用法
views = 75 * 0.01  # 假设 75% 的用户浏览了这个 item
favorites = 1
likes = 0
comments = ["非常棒的产品!", "超爱的", "下次还买"]
shares = 1
feedbacks = ["产品很好", "发货速度很快"]
rating = 5

composite_score = calculate_composite_score(views, favorites, likes, comments, shares, feedbacks, rating)
print("Composite Score:", composite_score)

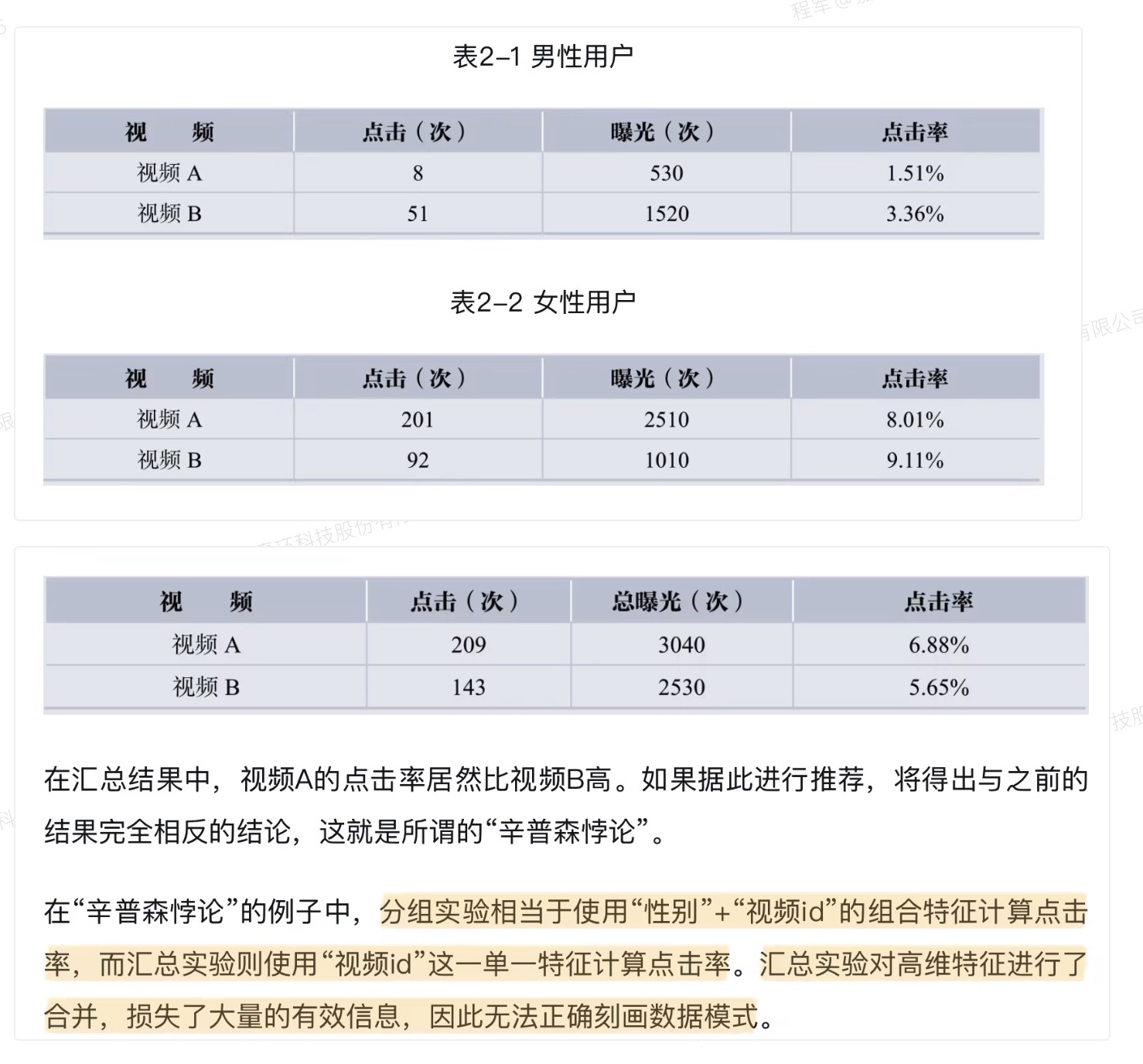
算法缺点

问题

这种融合的计算方式会导致辛普森悖论

改进方案

将 1-5 的分数值换成多维的评分向量，比如 [0.2, 0.3, 0.5, 0.1, 0.1]，这样每个维度的权重可以不同，当然计算时消耗的资源也会增加。

6.3 KiB Raw Permalink Blame History Unescape Escape